Jharkhand Board Class 9TH Science Notes | गति
JAC Board Solution For Class 9TH Science Chapter 8
1. एक वस्तु के द्वारा कुछ दूरी तय की गई। क्या इसका विस्थापन शून्य हो
सकता है ?. अगर हाँ, तो अपने उत्तर को उदाहरण के द्वारा समझाएँ।
उत्तर : हाँ, विस्थापन शून्य हो सकता है। यदि कोई वस्तु एवं वृत्ताकार पथ
पर एक पूर्ण चक्कर के लिए गति करता है तो उसके लिए गति का प्रारंभिक बिन्दु
एवं अंतिम बिन्दु एक ही होता है। अत: विस्थापन शून्य होता है।
2. किस अवस्था में किसी वस्तु के औसत वेग का परिमाण उसकी औसत
चाल के बराबर होगा?
उत्तर : यदि वस्तु द्वारा चली गई दूरी एवं विस्थापन का परिमाण एक समान
हो तो औसत वेग औसत चाल के बराबर होगा।
3. एक गाड़ी ओडोमीटर क्या मापता है?
उत्तर : ओडोमीटर स्वचालित वाहनों में वाहनों की चाल एवं चली गई दूरी
का माप करता है।
4. जब वस्तु एक समान गति में होती है तब इसका मार्ग कैसा दिखाई पड़ता
है ?
उत्तर : एक समान गति में चलती हुई वस्तु का पथ एकरेखीय दिखाई देता है।
5. किसी वस्तु के एकसमान व असमान गति के लिए समय-दूरी ग्राफ की
प्रकृति क्या होती है?
उत्तर : समान गति के लिए ग्राफ का स्वरूप एक सरल रेखा में होता है।
जबकि असमान गति के लिए यह वक्र रेखा में होता है।
6. किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका दूरी-समय
ग्राफ समय अक्ष के समानांतर एक सरल रेखा है?
उत्तर : यह वस्तु विरामावस्था में है क्योंकि यह वस्तु समय के साथ स्थान
परिवर्तन नहीं हो रहा है।
7. किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका
चाल-समय ग्राफ समय अक्ष के समानांतर एक सरल रेखा है?
उत्तर : यह वस्तु एक समान वेग से गतिशील है किन्तु इसमें त्वरण का मान
शून्य है।
8. वेग-समय ग्राफ के नीचे के क्षेत्र में मापी गई राशि क्या होती है?
उत्तर : यह क्षेत्रफल वस्तु द्वारा दिए गए समय अंतराल में कुल चली गई दूरी
के बराबर होता है।
9. निम्नलिखित में से कौन-सी अवस्थाएँ संभव हैं तथा प्रत्येक के लिए एक
उदाहरण दें―
(a) कोई वस्तु जिसका त्वरण नियत हो परन्तु वेग शून्य हो।
(b) कोई वस्तु किसी निश्चित दिशा में गति कर रही हो तथा त्वरण उसके
लंबवत् हो।
उत्तर : (a) जब वस्तु विराम की दशा में हो, तब यह स्थिति संभव है। (स्थिर
त्वरण शून्य है) (b) यह स्थिति संभव है। ऊंचाई से क्षैतिजाकार फेंकी गई गेंद की
चाल।
10. एकसमान गति से क्या तात्पर्य है? क्या आप ऐसी किसी वस्तु का उदाहरण
दे सकते हैं जिसकी गति एक समान हो?
उत्तर : एक समान गति वह विशेष गति है जिसमें गतिमान पिण्ड प्रति इकाई
समय में समान दूरी तय करती है। उदाहरण―घड़ी की सूई, अचर विभवान्तर पर
पंखे का घूमता हुआ डैना आदि।
11. सदिश राशियों के दो उदाहरण दीजिए।
उत्तर―(i) वेग, (ii) बल।
12. क्या चाल एक सदिश राशि है?
उत्तर―नहीं, चाल एक अदिश राशि है।
13. निम्न में से सदिश राशियाँ कौन-सी हैं–
द्रव्यमान, विस्थापन, चाल तथा वेग?
उत्तर― (i) विस्थापन, (ii) वेग।
14. चाल (या औसत चाल) का SI मात्रक क्या है?
उत्तर― मीटर/सेकेण्ड (ms⁻¹ )।
15. क्या एक अदिश राशि सदिश राशि में जोड़ी जा सकती है?
उत्तर―नहीं।
16. एकसमान गति के लिए त्वरण का क्या मान है?
उत्तर―शून्य।
17. दूरी-समय प्राफ क्या प्रदर्शित करता है?
उत्तर―चाल।
18. वेग तथा त्वरण के मात्रक लिखिए।
उत्तर―वेग का मात्रक : m/s तथा त्वरण का मात्रक : m/s²
19. विस्थापन को परिभाषित कीजिए।
उत्तर― किसी निश्चित दिशा में किसी वस्तु की स्थिति में हुए परिवर्तन को
विस्थापन कहते हैं।
20. रेखीय वेग तथा कोणीय वेग में सम्बन्ध लिखिए।
उत्तर― रेखीय वेग = कोणीय वेग × वृत्त का अर्द्धव्यास।
लघु उतरीय प्रश्न
1. एक वस्तु के द्वारा कुछ दूरी तय की गई। क्या इसका विस्थापन शून्य हो
सकता है? अगर हाँ, तो अपने उत्तर को उदाहरण के द्वारा समझाएँ।
उत्तर : हों, विस्थापन शून्य हो सकता है। यदि कोई वस्तु एवं वृत्ताकार पथ
पर एक पूर्ण चक्कर के लिए गति करता है तो उसके लिए गति का प्रारंभिक बिन्दु
एवं अंतिम बिन्दु एक ही होता है। अत: विस्थापन शून्य होता है।
2. चाल एवं वेग में अंतर बताइए।
उत्तर : चाल एवं वेग में अंतर―
चाल वेग
(ज) दूरी परिवर्तन की दर को चाल (i) विस्थापन परिवर्तन की दर को
कहते हैं। वेग कहते है।
(ii) चाल आदिश राशि है। (ii) वेग सदिश राशि है।
(iii) गतिमान वस्तु का चाल शून्य (iii) गतिमान वस्तु का वेग शून्य हो
नहीं होता है। सकता है।
(iv) दूरी में परिवर्तन से चाल में (iv) वेग में परिवर्तन विस्थापन की
परिवर्तन होता है। मात्रा या दिशा परिवर्तन के कारण
हो सकती है।
3. किस अवस्था में किसी वस्तु के औसत वेग का परिमाण उसकी औसत
चाल के बराबर होगा?
उत्तर : यदि वस्तु द्वारा चली गई दूरी एवं विस्थापन का परिमाण एक समान
हो तो औसत वेग औसत चाल के बराबर होगा।
4. आप किसी वस्तु के बारे में कब कहेंगे कि (i) वह एकसमान त्वरण से गति
में है? (ii) वह असमान त्वरण से गति में है?
उत्तर : (i) यदि किसी गतिमान वस्तु के वेग में परिवर्तन की दर समय के
छोटी-सी-छोटी अन्तराल के लिए भी हमेशा समान होता है तो वस्तु में उत्पन्न
त्वरण समरूप त्वरण कहलाता है।
(ii) यदि किसी गतिमान वस्तु के वेग में परिवर्तन की दर समय के विभिन्न
अन्तरालों में भिन्न-भिन्न है तो वस्तु में उत्पन्न त्वरण असमरूप त्वरण कहलाता है।
5. निम्नलिखित में से कौन-सी अवस्थाएँ संभव हैं तथा प्रत्येक के लिए एक
उदाहरण दें―
(a) कोई वस्तु जिसका त्वरण नियत हो परन्तु वेग शून्य हो।
(b) कोई वस्तु किसी निश्चित दिशा में गति कर रही हो तथा त्वरण उसके
लंबवत् हो।
उत्तर : (a) जब वस्तु विराम की दशा में हो, तब यह स्थिति संभव है। (स्थिर
त्वरण शून्य है)
(b) यह स्थिति संभव है। ऊँचाई से क्षैतिजाकार फेंकी गई गेंद की चाल।
6. विराम (Rest) किसे कहते हैं?
उत्तर―विराम किसी पिण्ड की वह स्थिति है जब समय परिवर्तन होने के बाद
भी पिण्ड के स्थान में कोई अन्तर नहीं आता है।
उदाहरणार्थ, विद्यालय भवन के निकट के पेड़ की दूरी दिन और तारीख बदलने
के बाद भी अचर होती है। अतः भवन और पेड़ दोनों विराम की स्थिति में हैं।
7. गति (Motion) किसे कहते हैं?
उत्तर― गति किसी पिण्ड की वह स्थिति है जब समय परिवर्तन के साथ-साथ
पिण्ड के स्थान में अन्तर आता रहता है।
उदाहरणार्थ, छात्र विद्यालय जाने के लिए जब घर से चलता है तो प्रति सेकेण्ड
उसके स्थान में अन्तर आता रहता है जिससे वह विद्यालय के निकट आता जाता
है। दौड़ता हुआ बालक, दौड़ती हुई गाड़ी, पेड़ से गिरता हुआ फल, बल्ला से
टकराने के बाद क्रिकेट का बॉल, भागता हुआ साँप आदि गतिमान पिण्ड माने जाते
हैं।
8. "विराम और गति सापेक्ष पद हैं।" कैसे?
उत्तर― विराम और गति सापेक्ष पद हैं क्योंकि कोई एक पिण्ड दूसरे पिण्ड
की तुलना में स्थान बदलकर गतिमान कहलाता है तो किसी तीसरे पिण्ड की अपेक्षा
वह विराम में रहता है।
उदाहरणार्थ, (i) पृथ्वी पर एक पेड़ किसी कुएँ की तुलना में विराम की स्थिति
में माना जाता है किन्तु सूर्य की तुलना में समूची पृथ्वी, पेड़ और कुओं सहित
गतिमान है, क्योंकि पृथ्वी अपने अक्ष पर घूमती भी है और सूर्य के चारों और
परिक्रमा भी लगाती है।
(ii) चलती ट्रेन का प्रत्येक मुसाफिर पटरी के बगल के किसी पेड़, गाँव खम्बा
की तुलना में गतिमान है, किन्तु एक यात्री सामने बैठे हुए यात्री की तुलना में विराम
की स्थिति में है तभी वह एक ही कागज पर रखे भोजन को साथ-साथ खा सकता है।
9. जन्तु और पौधों की गति में अन्तर स्पष्ट करें?
उत्तर―जन्तु और पौधों की गति में निम्नलिखित अन्तर है―(i) जन्तु अपने
शरीर के सम्पूर्ण या अंशतः भाग को इच्छा एवं आवश्यकतानुसार गतिमान रख
सकता है। जैसे-जन्तु दौड़ सकता है, हाथ हिला सकता है, पंख फड़फड़ा सकता
है। पौधे के सम्पूर्ण भाग की जगह कुछ विशेष भाग में ही गति पाई जाती है।
जैसे―फुनगी का पनपना, प्ररोह का बढ़ना, जड़ों की लम्बाई मिट्टी की ओर बढ़ना
आदि। (ii) जन्तु की गति प्रत्यक्षतः अनुभव किया जा सकता है जबकि पौधों में
उत्पन्न गति इतनी मन्द होती है कि उसे अनुभव करना भी कठिन हो जाता है। (iii)
जन्तु की गति का परिणाम किसी अंग विशेष में वृद्धि या हास नहीं होता है जबकि
पौधे के अंग बढ़कर अपना उपयोग या आकृति बदल लेते हैं। जैसे—पत्तागोभी,
फूलगोभी, सेब की आकृति में विकास।
10. मनुष्यों और जन्तुओं के द्वारा किस तरह की गति का प्रदर्शन किया जाता है?
उत्तर― मनुष्य और जन्तु अपने किसी खास अंगों की सहायता से सम्पूर्ण
शरीर का स्थान-परिवर्तन प्रत्यक्षतः कर पाने में समर्थ है। मानव की तरह पशु अपने
पैरों से चलते हैं, किन्तु पक्षी उड़ते है, साँप रेंगता है, चिड़ियाँ फुदकती है। कोई
जन्तु फाँदता है, कोई कूदता है, कोई छलांग लगाता है। एक लक्षण सबों में समान
होता है कि ये अपनी क्षमता से ही गति की अवस्था में आते हैं और मार्ग एवं सुविधा
के अनुसार तेज या मन्द गति उत्पन्न करते है। चोर भागता है, बूदा टहलता है,
मछलियाँ डुबकी लगाती है। मनुष्य और जन्तु अपने किसी खास अंग में भी गति
ला सकते हैं जैसे-ताली बजाना, पैर पटकना, गर्दन हिलाना आदि।
11. परिभाषित करें―
(i) औसत चाल, (ii) सदिश और अदिश राशियाँ, (iii) आपेक्षिक वेग,
(iv) रेखीय वेग, (v) कोणीय वेगा
उत्तर―(i) औसत चाल― जब कोई वस्तु असमान गति से चल रही होती
है तो औसत चाल वस्तु द्वारा चली गई कुल दूरी तथा इस दूरी को चलने में लगे
समय का अनुपात है।
औसत चाल = वस्तु द्वारा चली गई दूरी (S)/इस दूरी को तय करने में लिया गया कुल समय (t)
जैसे―एक बस राँची से पटना तक 320 km की दूरी 8 घंटे में तय करती
है तो उसकी औसत चाल निम्न प्रकार ज्ञात करते है।
बस की औसत चाल = तय की गई कुल दूरी/दूरी का तय करने में लिया गया समय
= 320/8 = 40 km/h.
(ii) सदिश और अदिश राशियाँ― सदिश राशियाँ वे है जिन्हें परिणाम और
दिशा दोनों होते हैं और वे सदिश के योग के नियम का पालन करते है।
अदिश राशियों वे है जिन्हें केवल परिणाम होता है, उन्हें दिशा नहीं होती।
अदिश राशियों का जोड़, घटाव या गुणा साधारण अंकगणित के नियमों के अनुसार
होता है।
(iii) आपेक्षिक वेग―जब दो वस्तुएँ गतिमान हो, तो उनमें किसी एक का,
दूसरी की अपेक्षा जो वेग होता है, वह आपेक्षिक वेग कहा जाता है।
(iv) रेखीय वेग―किसी वस्तु के स्थान परिवर्तन की समय-दर को उसका
रेखीय वेग कहते है। उसे v से निरूपित करते हैं। इसका S.I मात्रक m/s
मोटर/सेकेण्ड) होता है।
(v) कोणीय वेग― किसी वृत्त के केन्द्र से उसकी परिधि पर चल रही वस्तु
को मिलाने वाली त्रिज्या (ध्रुवांतर रेखा) द्वारा घुमे गए कोण को समय-दर को उसका
कोणीय वेग कहते हैं। इसे ω (ओमेगा) से निरूपित करते हैं और इसका S.Ι मात्रक
rad/sec (रेडियन/सेकेण्ड) होता है।
12. क्या एक समान वृत्तीय गति त्वरित गति है? यदि
है, तो त्वरण की दिशा क्या होगी?
उत्तर― हाँ। एकसमान वृत्तीय गति में वेग को सिर्फ दिशा में परिवर्तन होता है।
वेग का परिणाम नहीं बदले के लिए त्वरण की दिशा वेग की दिशा के अभिलंब
तो वेग को दिशा स्पर्शरेखा की दिशा में होती है (पाश्वांकित चित्र), इसलिए त्वरण
की दिशा वृत्त के केन्द्र ओर होगी।
13. निम्नलिखित में अन्तर स्पष्ट करें―
(i) दूरी और विस्थापन,
(ii) सदिश और अदिश,
(iii) एक समान रेखीय गति और एक समान वृत्तीय गति,
(iv) रेखीय वेग और कोणीय वेगा
उत्तर―(i) दूरी और विस्थापन के बीच अन्तर―विस्थापन दो बिन्दुओं
के बीच न्यूनतम दूरी है, जिसके साथ संबद्ध दिशा भी सम्मिलित रहती है,
जबकि दूरी दो बिन्दुओं को मिलाने वाले किसी भी मार्ग की
सम्बाई है।
माना कोई कण बिन्दु A से बिंदु D तक मार्ग A'B'C'D' तक करके
पहुँचता है। यहाँ कण द्वारा तय की गई कुल दूरी मार्ग A'B'C'D' की लम्बाई के
बराबर है। यदि कण A' से D' की ओर दिशा A'D' में चलकर पहुँचता है तो
मार्ग A'D' प्रारम्भिक स्थिति A' से अन्तिम स्थिति D' तक पहुँचने का सबसे
छोटा मार्ग है। कण द्वारा A'D' दिशा में चली गई दूरी AD विस्थापन कहलाती है
तथा इसे सदिश A'D' के द्वारा व्यक्त करते हैं।
(ii) अदिश राशि और सदिश राशि में अन्तर ―
अदिश राशि सदिश राशि
(i) अदिश एक भौतिक राशि है, (i) सदिश एक भौतिक राशि है,
जिसमें केवल परिणाम होता है। जिसमें परिमाण के साथ-साथ
संबद्ध दिशा भी सम्मिलित होती
है।
(ii) अदिश राशियों को बीजगणित के (ii) सदिश राशियों को बीज गणित के
एक साधारण नियम के अनुसार साधारण नियम के अनुसार नहीं
जोड़ा जा सकता है। जोड़ा जा सकता है।
(iii) अदिश राशि को किसी भी दिशा में (iii) सदिश किसी तीर के निशान से
खींची गई सरल रेखा से निरूपित निरूपित किया जा सकता है। तीर
किया जा सकता है। सरल रेखा की में सरल रेखा की लम्बाई सदिश के
लम्बाई अदिश का परिमाण व्यक्त परिणाम तथा तीर का चिह्न उसकी
करती है। दिशा को निरूपित करता है।
(iv) लम्बाई, द्रव्यमान, क्षेत्रफल, (iv) विस्थापन, वेग, संवेग, बल आदि
आयतन, घनत्व दूरी आदि अदिश सदिश राशि के उदाहरण है।
राशि के उदाहरण है।
(iii) एकसमान रेखीय गति और एकसमान वृत्तीय गति में अन्तर—
एकसमान रेखीय गति―यदि कोई गतिमान वस्तु किसी सरल रेखीय पथ
पर इस प्रकार गति करे कि उसके द्वारा समान समय में समान दूरी तय की जाए,
तो वस्तु की गति एक समान रेखीय गति कहलाती है। इस प्रकार की गति में चाल
का परिमाण समान रहता है तथा गति की दिशा भिन्न-भिन्न बिन्दुओं पर परिवर्तित
नही होती है। अत: एकसमान रखीय गति में वस्तु का त्वरण होता है।
एकसमान वृत्तीय गति― जब कोई वस्तु इस प्रकार गति करती है कि उसका
पथ वृत्ताकार हो तथा उसकी चाल एकसमान हो, तो वस्तु की गति एकसमान वृत्तीय
गति कहलाती है।
यद्यपि वस्तु की चाल का परिमाण समान रहता है, परन्तु गति की दिशा प्रत्येक
बिन्दु पर परिवर्तित होती रहती है। दिशा में यह परिवर्तन वस्तु में त्वरण उत्पन्न
करता है।
(iv) रेखीय वेग और कोणीय वेग में अन्तर―
रेखीय वेग―किसी गतिमान पिण्ड के स्थान परिवर्तन की समय-दर को
उसका रेखीय वेग कहते हैं। इसे सामान्यतः v से सूचित करते हैं और इसका मात्रक
मीटर/सेकेण्ड होता है।
कोणीय वेग―किसी वृत्त के केन्द्र से उसकी परिधि पर गतिमान कण को
मिलाने वाली त्रिज्या (ध्रुवांतर रेखा) द्वारा घूमे हुए कोण की समय-दर को उस गतिमान
कण का कोणीय वेग कहते हैं। इसे सामान्यतः 0 से सूचित करते हैं। तथा इसका
मात्रक रेडियन/सेकेण्ड होता है।
14. त्वरण और मंदन किसे कहते हैं? इसके लिए सूत्र तथा मात्रक लिखें।
उत्तर―त्वरण―किसी गतिमान पिण्ड के वेग में परिवर्तन की दर को त्वरण
कहते हैं।
मंदन―ऋणात्मक त्वरण को मंदन कहते हैं जो घटते हुए वेग से गतिमान
पिण्ड के वेग के घटने की दर बतलाती है।
त्वरण का सूत्र है a = v–u/t
या, त्वरण = अंतिम वेग – प्रारंभिक वेग/समय = वेग में अन्तर/समय
त्वरण का मात्रक मीटर प्रति सेकेण्ड अर्थात् मीटर/सेकेण्ड² है।
दीर्घ उत्तरीय प्रश्न
1. गति के समीकरणों को लिखकर उन्हें प्राप्त करें।
उत्तर-गति के तीन प्रमुख समीकरण हैं―
(i) v = u+at (ii) s = ut+1/2at² तथा (iii) v² = u² + 2as
जहाँ, u = प्रारम्भिक वेग, v = अंतिम वेग, t= समय, a = त्वरण,
2 = दूरी का संकेत है।
इन तीनों समीकरणों को निम्न चरणों में स्थापित कर सकते हैं
(i) मान लिया कि किसी पिण्ड का प्रारम्भिक वेग u और त्वरण a है।
1 सेकेण्ड बाद पिण्ड का वेग = u+a
2 सेकेण्ड बाद पिण्ड का वेग =u+2a
3 सेकेण्ड बाद पिण्ड का वेग =u+ at
यदि पिण्ड का वेग । सेकेण्ड के बाद v हो जाए तो v = u+at
2. ग्राफीय विधि से साबित करें कि
(i) v = u+at, (ii) s = ut+1/2at²
तथा (iii) v² = u²+2as जहाँ u,v,a,t और s अपना सामान्य अर्थ रखते
हैं।
उत्तर―मान लिया कि किसी समयांतराल के प्रारंभ में किसी वस्तु का वेग u तथा
समयांतराल t के अंत में v है। यदि वस्तु एक समान वेग से जा रही है तो इसका
(i) प्रथम समीकरण (एकसमान त्वरण a के साथ सरल रेखा पर गतिमान वस्तु
द्वारा समय t में प्राप्त वेग—
वेग-समय ग्राफ से, त्वरण a = रेखा BA की ढाल = AC/BC
या, AC = a × BC .
समयांतराल t के अंत में वेग
v=AD=CD + AD = OB+ AC(∴ CD =OB)
=u+a × BC = u+at (∴ BC=OD= t)
∴ v = v + at
(ii) द्वितीय समीकरण (एकसमान त्वरण a के साथ रेखा पर गतिमान वस्तु
द्वारा समय । में तय की हुई दूरी)―वेग-समय ग्राफ से, O से t समयांतराल में
तय की हुई दूरी s छायांकित (shaded) भाग के क्षेत्रफल के बराबर होगी।
दूरी s = समलंब चतुर्भुज OBAD का क्षेत्रफल = आयत OBCD का क्षेत्रफल
+ त्रिभुज ABC का क्षेत्रफल
(iii) तृतीय समीकरण (एकसमान त्वरण के साथ रेखा पर गतिमान वस्तु
द्वारा दूरी तय करने में प्राप्त वेग)―
3. चाल-समय आरेख से निम्नलिखित को आप किस तरह प्राप्त करोगे? (क)
त्वरण, (ख) निश्चित समय में तय की गई दूरी।
उत्तर―माना चाल-समय आरेख के दो प्रतिरूप निम्नांकित है―
(i) जब चाल बढ़ती हो और
(ii) जब चाल घटती हो
चित्र-आरेख से, त्वरण = प्रवणता = AB/BC
(ख) परिभाषा के अनुसार,
तय की गई दूरी = औसत चाल × समय
किन्तु निश्चित समय t में तय की गई दूरी
= आरेख का कुल क्षेत्रफल
= ∆ABC का क्षेत्रफल
= 1/2 आधार × ऊँचाई = 1/2 BC ×AC
= 1/2 × t × v = 1/2vt.
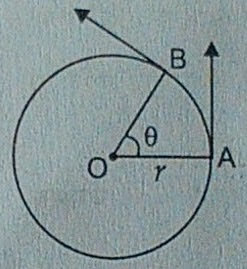
4. वृत्तीय गति में सरल रेखीय गति और कोणीय वेग में सम्बन्ध स्थापित करें।
अथवा, सूत्र v = rω को स्थापित करें।
उत्तर : सरल रेखीय तथा कोणीय वेग में संबंध―
मान लिया कि पार्श्वांकित आकृति में,
O वृत्त का केन्द्र है। , r वृत्त की त्रिज्या है।
A कोई कण है जो वे से परिधि पर चलता है और t समय के बाद B पर पहुँच जाता है।
ₛAB की दूरी है। θ केन्द्र पर कोण है। (मान लिया)
ω (आमेगा) कोणीय वेग है।
हम जानते हैं कि रेखीय वेग = वेग/समय या, v = s/t या,s= vt .......(1)
अब ज्यामिति से केन्द्रीय कोण = चाप/त्रिज्या या, v = s/r या, s = θr .....(2)
अब समीकरण (1) = (2) ∴ vt= θr या, v/r = θ/t ........(3)
अब कोणीय वेग की परिभाषा से कोणीय वेग = केन्द्र पर का कोण/समय
या, ω = θ/t ........(4)
अब समीकरण (3) = (4); v/r = ω अतः v = ωr या, v = rω
अर्थात् रेखीय वेग = त्रिज्या कोणीय वेग × वृत्ताकार पथ की अभीष्ट संबंध
हुआ।
◆◆